
The dining philosophers problem has been a famous computer science problem for half a century. When first presented, the challenge was simply to find a solution that did not deadlock. I.e. a solution where none of the diners starved to death in the process of waiting for a chance to eat.
This paper presents four solutions to the problem, and compares the performance of each solution. Additionally the impact of the number of diners, and the number of processors is explored to see how these factors impact overall performance. And finally, an alternate topology, where each diner requires 3 forks to eat, is explored with these same 4 algorithms. It will be shown that there is a single algorithm that consistently performs as well as, or better than, the other 3 algorithms, as all factors are varied (number of processors, number of diners, topology).
The complete C++11 source code for this study is included in this paper so that others may easily confirm or refute the results presented herein.
A practical application of the results of this study is the algorithm
underlying the std::lock(L1, L2, ...) function in section 30.4.3
[thread.lock.algorithm] of the C++11 and C++14 standards:
template <class L1, class L2, class... L3> void lock(L1&, L2&, L3&...);Requires: Each template parameter type shall meet the
Lockablerequirements, [Note: Theunique_lock>class template meets these requirements when suitably instantiated. — end note]Effects: All arguments are locked via a sequence of calls to
lock(),try_lock(), orunlock()on each argument. The sequence of calls shall not result in deadlock, but is otherwise unspecified. [Note: A deadlock avoidance algorithm such as try-and-back-off must be used, but the specific algorithm is not specified to avoid over-constraining implementations. — end note] If a call tolock()ortry_lock()throws an exception,unlock()shall be called for any argument that had been locked by a call tolock()ortry_lock().
Indeed, all of the test software used by this paper will call
::lock to obtain "forks" (lock two or three
std::mutexes). One can safely assume that ::lock()
in this paper represents nothing but example implementations of
std::lock().
This Wikipedia link has a great description of the problem. If you haven't read it yet, read it now. I'll wait...
Ok, now that we're all on the same page (and back on this one), I'll explain the minor deviations that this paper takes, and why.
As it turns out, any algorithm that solves this problem without deadlock, will perform wonderfully when the philosophers spend any appreciable amount of time thinking, compared to eating. I.e. they can each think independently (that is what makes them philosophers after all). When they do as much thinking as they do eating, we call this a low contention scenario because the philosophers spend relatively little time contending for the forks.
However when the philosophers are all really hungry, they tend to eat more and think less (just like the rest of us). This means they spend more time contending for the forks, and subsequently the nature of the algorithm which arbitrates who gets what fork when, becomes more and more important. In the limit, as thinking time goes to zero, the importance of the algorithm which hands out the forks becomes paramount, and dominates the performance of the entire meal (the application).
Therefore in the tests included herein:
::lock() algorithm.
The actual order the forks are obtained is encapsulated within the
::lock() algorithm.These parameters have been chosen to highlight the performance differences between the 4 algorithms presented herein, and to somewhat approximate a real-world high-contention scenario. If the scenario is low-contention, the algorithm does not matter, as long as it avoids deadlock.
For each solution, the forks are represented as a
vector<mutex>:
std::vector<std::mutex> table(nt);
There is a class Philosopher which will reference two (or three)
mutexes, and the table setting is represented as a
vector<Philosopher>:
std::vector<Philosopher> diners;
The ordered solution is the one originally proposed by Edsger Dijkstra in
1965. One assigns an order to the forks (we will use their address in the
vector), and each Philosopher will first lock the
lower-numbered mutex, and then lock the higher-numbered
mutex.
The two-mutex variant of lock can be coded like so
if we assume that the template parameter L0 is always a
std::unique_lock (which is not a good assumption for
std::lock but we overlook that detail here).
template <class L0>
void
lock(L0& l0, L0& l1)
{
if (l0.mutex() < l1.mutex())
{
std::unique_lock<L0> u0(l0);
l1.lock();
u0.release();
}
else
{
std::unique_lock<L0> u1(l1);
l0.lock();
u1.release();
}
}
The purpose of the internal use of std::unique_lock<L0> is
to make the code exception safe. If the second lock() throws,
the local std::unique_lock<L0> ensures that the first lock
is unlocked while propagating the exception out.
Note that this algorithm has a very predictable code flow. There are only two ways to get the job done, and there are no loops.
No one that I'm aware of has seriously proposed this algorithm as a good
solution. However it is included here as there is at least one shipping
implementation of std::lock that implements this exact algorithm.
Furthermore, a naive reading of the C++ specification for
std::lock has led more than one person to believe that this is
the only algorithm possible which will conform to the C++ specification.
Nothing could be further from the truth.
This algorithm is called "persistent" as the Philosopher simply
doggedly locks one mutex, and then try_lock() the
others. If the try_lock()s succeed, he is done, else he unlocks
everything, and immediately tries the exact same thing again, and again, and
again, until he succeeds.
This is simple to code for the two-mutex variant as:
template <class L0, class L1>
void
lock(L0& l0, L1& l1)
{
while (true)
{
std::unique_lock<L0> u0(l0);
if (l1.try_lock())
{
u0.release();
break;
}
}
}
Results will later show that this algorithm, while not ideal, actually performs relatively well when there is plenty of spare processing power. Or said differently, the algorithm works, but is power hungry.
A simple but important variation of the persistent
algorithm is when a try_lock() fails, then block on that
mutex. This eliminates a lot of useless spinning, thus
consuming less power, and thus leaving more processing power available to
other diners. As it turns out, a diner needs not only forks to eat, he also
needs an available processor. If you don't have the forks, don't waste power.
This is simple to code for the two-mutex variant as:
template <class L0, class L1>
void
lock(L0& l0, L1& l1)
{
while (true)
{
{
std::unique_lock<L0> u0(l0);
if (l1.try_lock())
{
u0.release();
break;
}
}
{
std::unique_lock<L1> u1(l1);
if (l0.try_lock())
{
u1.release();
break;
}
}
}
}
This algorithm still contains a theoretical infinite loop. However it will
go through this loop rather slowly, as each mutex locked besides
the very first, is one for which the thread has just failed a call to
try_lock() (and so the subsequent lock() is likely
to block).
Some people have expressed a great deal of concern about livelock with this algorithm. And indeed experiments have revealed a very small amount of temporary livelock can occur under high-contention conditions as emphasized by the tests herein. The 4th algorithm is designed to reduce this small amount of experimentally observed livelock to zero.
This algorithm is a minor variant of the smart
algorithm. It has experimentally shown small performance advantages over the
smart algorithm on OS X. After the thread has failed a
try_lock() on a mutex, but prior to blocking on
that mutex, yield the processor to anyone else who might need
it. Results may be different on other OS's. But on OS X, it is just the
polite thing to do. And the system as a whole (though not the individual
Philosopher) benefits under conditions where processing power is
already maxed out.
template <class L0, class L1>
void
lock(L0& l0, L1& l1)
{
while (true)
{
{
std::unique_lock<L0> u0(l0);
if (l1.try_lock())
{
u0.release();
break;
}
}
std::this_thread::yield();
{
std::unique_lock<L1> u1(l1);
if (l0.try_lock())
{
u1.release();
break;
}
}
std::this_thread::yield();
}
}
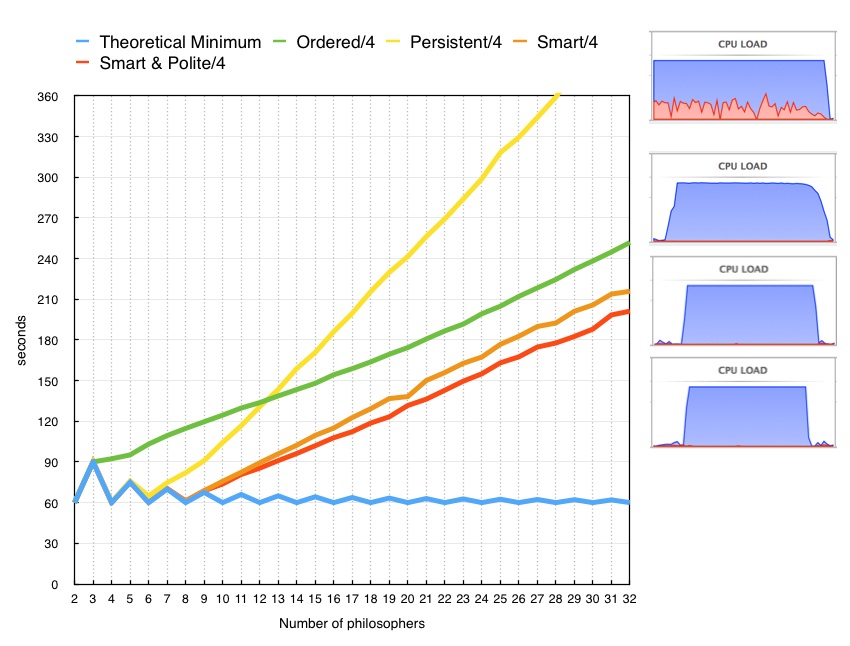
In the figure to the right I have set up 31 tests. Each test has a number of
philosophers seated at a round table. The number of philosophers varies from
2 to 32. There is one fork (mutex) between every two adjacent
philosophers. Each philosopher must obtain his two adjacent forks in order
to eat. This test shows timing results for a 4 processor Intel Core i5 running
Apple OS X 10.9.2.
The vertical axis represents the total number of seconds it takes for all philosophers at the table to get a total of 30 seconds each of "quality fork time."
When there are only two philosophers at the table, it seems clear that only one of them can eat at a time, and thus it will take 60 seconds for each of them to eat for 30 seconds. This is true whether that each eat for 30 seconds at a time, or if they each eat for a few milliseconds at a time.
The chart shows in blue a theoretical minimum amount of time the meal must take for everyone to get 30 seconds. When there is a even number of philosophers at the table, it is easy to see that every other philosopher can eat at one time (say the even numbered philosophers if you numbered them). And then the odd-numbered philosophers can eat. Whether they all eat for a few milliseconds or 30 seconds each, it should take no more than 60 seconds for everyone to get a full meal, assuming one has a sufficient number of processors to supply to each philosopher whenever he needs one (has obtained two forks).
When the number of philosophers at the table is odd, it can be shown that the theoretical minimum meal time is 30 * N /((N-1)/2) seconds. When N is 3, it is easy to see that there is no room for concurrency. Just like the N == 2 case, only one philosopher can eat at a time. Thus the minimum meal time is 90 seconds. For higher odd numbers of philosophers at the table, the minimum time actually drops, and approaches 60 seconds as N goes to infinity.
All 4 algorithms nail the N == 2, and N == 3 cases. However, with N >= 4, the ordered algorithm breaks away from the theoretical minimum and climbs in a close to linear fashion with the number of dining philosophers. This essentially represents the algorithm's lack of ability to evenly distribute processing power equally to each philosopher. To the right of the chart are CPU Load graphics, one for each algorithm at the N == 32 case. The second from the top is for the ordered algorithm. In this figure one can see that the cpu load tapers off somewhat at the end of the test, indicating that towards the end there are fewer and fewer philosophers that are still hungry. This also indicates that those still-hungry philosophers were experiencing mild starvation earlier in the test (else they would not still be hungry).
The persistent algorithm starts off outperforming the ordered algorithm. Up through N == 5, the results are virtually indistinguishable from the theoretical minimum. And up through N == 7, the results are only slightly worse than the theoretical minimum. But by N == 8, the cost of this algorithm starts to sharply rise as more philosophers come to the table. The rise is so sharp that the algorithm begins to get outperformed by the ordered algorithm by N == 13. The top cpu load graphic indicates that a significant portion of the cpu is spent in system calls (the red area), which is consistent with the notion that this algorithm is needlessly locking and unlocking mutexes without getting any real work (eating) done.
The smart and smart & polite algorithms have very similar performance. They both perform identically to the theoretical minimum up through N == 9. This is the point that even with a perfectly fair distribution of processing power, the philosophers start collectively asking for more than 4 cpus. As the number of philosophers increases, the slope of the smart & polite algorithm is slightly less than the smart algorithm, and appears equal to the slope of the ordered algorithm. Note that in the CPU load factor graphics for these two algorithms, the meal ends relatively abruptly, with all philosophers finishing at about the same time. Indeed, the success of these algorithms resides in the fact that all philosophers are treated equally during the meal, none getting starved any more than the others.
The question naturally arises now:
How do these results scale with the number of processors?
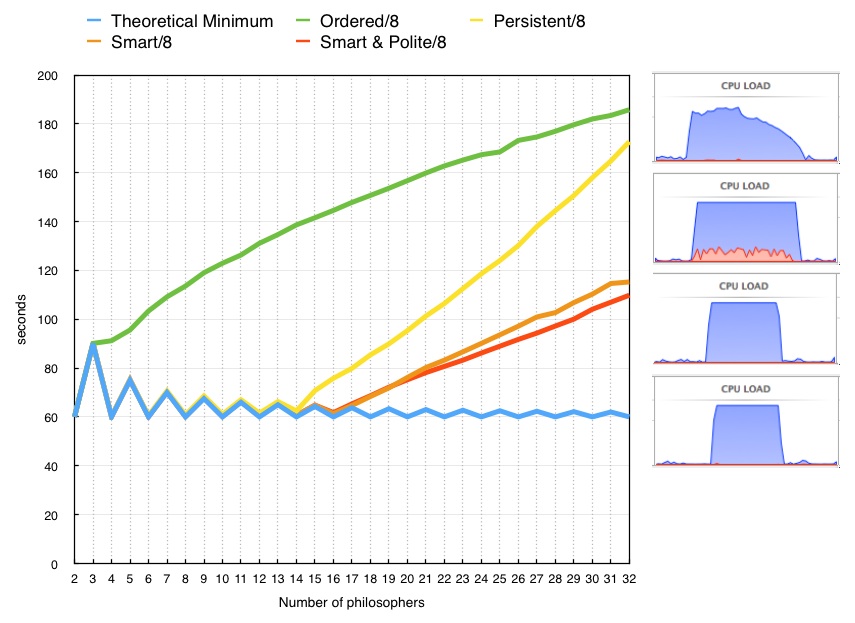
As luck would have it, I have an 8 core Intel Core i7 running Apple OS X 10.9.2 available to run the exact same code.
The results are qualitatively the same.
The ordered algorithm again breaks from the minimum at N == 4, and rises. The rise is not as rapid as on the 4 core machine, but neither is the performance twice as fast.
The persistent algorithm sticks to the theoretical minimum up to about N == 13, and then sharply rises. The rise is sharp enough such that the ordered algorithm will eventually outperform it, but that no longer happens below N == 32. The CPU load graphic again shows excessive cpu devoted to system calls.
The smart and smart & polite algorithms stay on the theoretical minimum out to 17 philosophers, and then rise approximately linearly.
The smart & polite algorithm is consistently the highest performing algorithm, or at the very least, never outperformed by any of the other 3 algorithms. Concerns of any significant livelock are not supported by these results. Though please feel free to run this test on your own machine and publicly report your results.
The next question to naturally arise is:
How do these results scale with the number of mutexes one needs to lock?
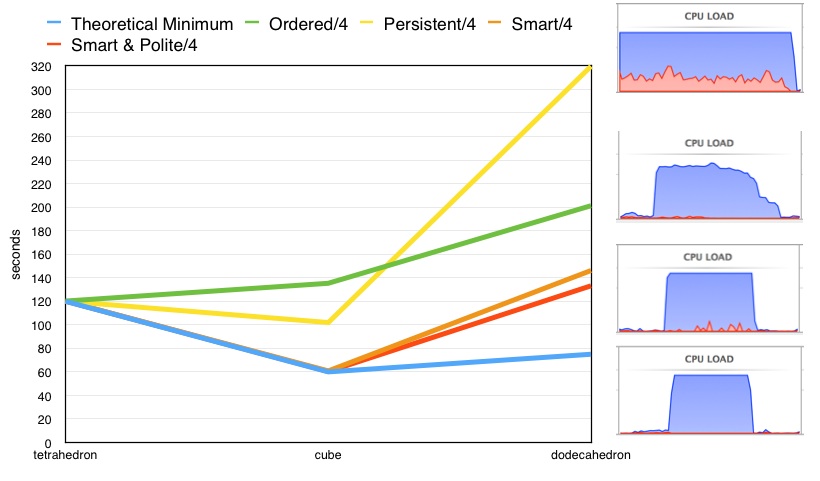
Though not a complete answer, I have created a partial answer to the above question which should shed some light.
Instead of the philosophers sitting at a round table, imagine they are each seated at a vertex of a Platonic solid. And further imagine that we restrict ourselves to those solids for which each vertex is the intersection of exactly 3 faces (and thus 3 edges). And finally imagine that there is a fork at the middle of each edge.
Due to the limits of both Euclidean geometry, and my visualization abilities, this experiment will take on only 3 forms:
In order to eat, each philosopher must obtain all 3 of his adjacent forks.
The tetrahedron case is like the 2 and 3 philosopher round table case. It is impossible for two or more philosophers to eat at once, and so the best that can be done is for the 4 philosophers to each eat by themselves (30 seconds each) for a total of 120 seconds. All 4 algorithms nail this degenerate case.
The cube case is easy to analyze. Four of the eight philosophers can eat at any one time. Thus in two 30 second time slots, everyone can get a full tummy. However only the smart, and smart & polite algorithms are able to achieve this minimum (with 4 cores). The persistent and ordered algorithms are both significantly slower than this. As we saw in the 2-D tests, the ordered algorithm is never faster than the degenerate sequential case.
As we move to the dodecahedron, 4 cores are not enough for even the smart and smart & polite algorithms to stay at the theoretical minimum. But the smart & polite shows a small advantage over the smart algorithm. A small amount of livelock is visible on the smart algorithm's CPU load graphic (3rd from the top), visualized by the bits of red.
The ordered algorithm running on the dodecahedron shows a relatively gradual "trailing off" slope in the CPU load graphic, indicating mild starvation, and thus penalizing the performance of the algorithm.
The persistent algorithm running on the dodecahedron performs the worst. In the CPU load graphic a significant amount of cpu wasted on system calls is quite evident.
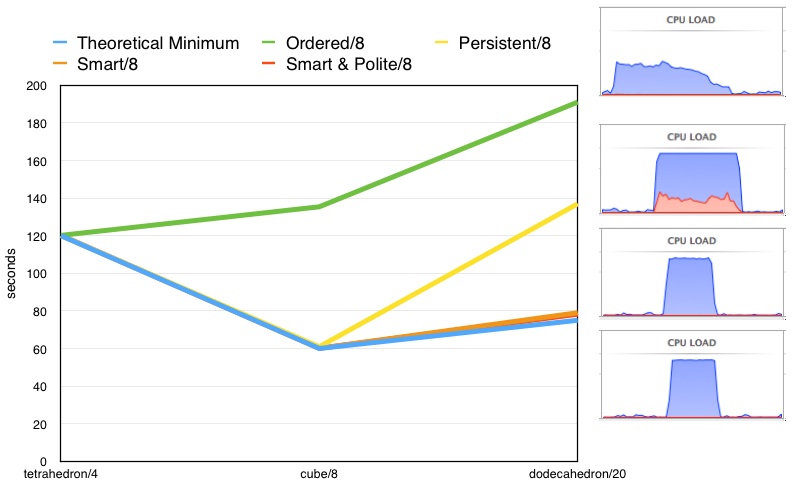
Running the same test on an 8 core machine is qualitatively the same but with a few differences worth pointing out:
The persistent algorithm now has enough processing power to nail the theoretical minimum on the cube.
The slope of the expense of the persistent algorithm from the cube to the dodecahedron appears greater than that of the ordered algorithm, and thus would likely eventually become more expensive than the ordered algorithm as more philosophers are added.
The smart and smart & polite algorithms now have enough processing power to very nearly nail the theoretical minimum on the dodecahedron. This theoretical minimum requires 8 processors, so this machine is just on the edge of delivering that minimum.
Concerns of any significant livelock appear to be 100% addressed by the smart & polite algorithm. Please feel free to run this test on your own machine and publicly report your results.
Four algorithms have been presented and performance tested on 4 and 8 core
machines, and under a variety of tests. Each of these four algorithms is a
different implementation for std::lock() for the two and three
mutex locking case. An algorithm termed herein as smart
& polite has been shown to never be worse than any other algorithm,
and often significantly superior.
The smart & polite algorithm attempts to lock the first mutex in the group and then try-lock the rest. If any mutex fails the try-lock, everything is unlocked, a call to yield is made, and then the algorithm repeats except that the mutex that previously failed the try-lock is the first one locked. Code is given for the 2 and 3 mutex cases. Expanding this algorithm to N variadic mutexes is left as an exercise for the reader, but has been implemented in libc++ (i.e. it is not unreasonably difficult).
#include <chrono>
#include <mutex>
#include <random>
#include <array>
#include <vector>
#include <thread>
#include <iostream>
#ifdef SMART_POLITE
template <class L0, class L1>
void
lock(L0& l0, L1& l1)
{
while (true)
{
{
std::unique_lock<L0> u0(l0);
if (l1.try_lock())
{
u0.release();
break;
}
}
std::this_thread::yield();
{
std::unique_lock<L1> u1(l1);
if (l0.try_lock())
{
u1.release();
break;
}
}
std::this_thread::yield();
}
}
#elif defined(SMART)
template <class L0, class L1>
void
lock(L0& l0, L1& l1)
{
while (true)
{
{
std::unique_lock<L0> u0(l0);
if (l1.try_lock())
{
u0.release();
break;
}
}
{
std::unique_lock<L1> u1(l1);
if (l0.try_lock())
{
u1.release();
break;
}
}
}
}
#elif defined(PERSISTENT)
template <class L0, class L1>
void
lock(L0& l0, L1& l1)
{
while (true)
{
std::unique_lock<L0> u0(l0);
if (l1.try_lock())
{
u0.release();
break;
}
}
}
#elif defined(ORDERED)
template <class L0>
void
lock(L0& l0, L0& l1)
{
if (l0.mutex() < l1.mutex())
{
std::unique_lock<L0> u0(l0);
l1.lock();
u0.release();
}
else
{
std::unique_lock<L0> u1(l1);
l0.lock();
u1.release();
}
}
#endif
class Philosopher
{
std::mt19937_64 eng_{std::random_device{}()};
std::mutex& left_fork_;
std::mutex& right_fork_;
std::chrono::milliseconds eat_time_{0};
static constexpr std::chrono::seconds full_{30};
public:
Philosopher(std::mutex& left, std::mutex& right);
void dine();
private:
void eat();
bool flip_coin();
std::chrono::milliseconds get_eat_duration();
};
constexpr std::chrono::seconds Philosopher::full_;
Philosopher::Philosopher(std::mutex& left, std::mutex& right)
: left_fork_(left)
, right_fork_(right)
{}
void
Philosopher::dine()
{
while (eat_time_ < full_)
eat();
}
void
Philosopher::eat()
{
using Lock = std::unique_lock<std::mutex>;
Lock first;
Lock second;
if (flip_coin())
{
first = Lock(left_fork_, std::defer_lock);
second = Lock(right_fork_, std::defer_lock);
}
else
{
first = Lock(right_fork_, std::defer_lock);
second = Lock(left_fork_, std::defer_lock);
}
auto d = get_eat_duration();
::lock(first, second);
auto end = std::chrono::steady_clock::now() + d;
while (std::chrono::steady_clock::now() < end)
;
eat_time_ += d;
}
bool
Philosopher::flip_coin()
{
std::bernoulli_distribution d;
return d(eng_);
}
std::chrono::milliseconds
Philosopher::get_eat_duration()
{
std::uniform_int_distribution<> ms(1, 10);
return std::min(std::chrono::milliseconds(ms(eng_)), full_ - eat_time_);
}
int
main()
{
#ifdef SMART_POLITE
std::cout << "SMART_POLITE\n";
#elif defined(SMART)
std::cout << "SMART\n";
#elif defined(PERSISTENT)
std::cout << "PERSISTENT\n";
#elif defined(ORDERED)
std::cout << "ORDERED\n";
#endif
for (unsigned nt = 2; nt <= 32; ++nt)
{
std::vector<std::mutex> table(nt);
std::vector<Philosopher> diners;
for (unsigned i = 0; i < table.size(); ++i)
{
int j = i;
int k = j < table.size() -1 ? j+1 : 0;
diners.push_back(Philosopher(table[j], table[k]));
}
std::vector<std::thread> threads(diners.size());
unsigned i = 0;
auto t0 = std::chrono::high_resolution_clock::now();
for (auto& t : threads)
{
t = std::thread(&Philosopher::dine, diners[i]);
++i;
}
for (auto& t : threads)
t.join();
auto t1 = std::chrono::high_resolution_clock::now();
using secs = std::chrono::duration<float>;
std::cout << "nt = " << nt << " : " << secs(t1-t0).count() << std::endl;
}
}
#include <chrono>
#include <mutex>
#include <random>
#include <array>
#include <vector>
#include <thread>
#include <algorithm>
#include <iostream>
#ifdef SMART_POLITE
template <class L0, class L1, class L2>
void
lock(L0& l0, L1& l1, L2& l2)
{
int i = 0;
while (true)
{
switch (i)
{
case 0:
{
std::unique_lock<L0> u0(l0);
i = std::try_lock(l1, l2);
if (i == -1)
{
u0.release();
return;
}
}
++i;
std::this_thread::yield();
break;
case 1:
{
std::unique_lock<L1> u1(l1);
i = try_lock(l2, l0);
if (i == -1)
{
u1.release();
return;
}
}
if (i == 1)
i = 0;
else
i = 2;
std::this_thread::yield();
break;
case 2:
{
std::unique_lock<L2> u2(l2);
i = try_lock(l0, l1);
if (i == -1)
{
u2.release();
return;
}
}
std::this_thread::yield();
break;
}
}
}
#elif defined(SMART)
template <class L0, class L1, class L2>
void
lock(L0& l0, L1& l1, L2& l2)
{
int i = 0;
while (true)
{
switch (i)
{
case 0:
{
std::unique_lock<L0> u0(l0);
i = std::try_lock(l1, l2);
if (i == -1)
{
u0.release();
return;
}
}
++i;
break;
case 1:
{
std::unique_lock<L1> u1(l1);
i = try_lock(l2, l0);
if (i == -1)
{
u1.release();
return;
}
}
if (i == 1)
i = 0;
else
i = 2;
break;
case 2:
{
std::unique_lock<L2> u2(l2);
i = try_lock(l0, l1);
if (i == -1)
{
u2.release();
return;
}
}
break;
}
}
}
#elif defined(PERSISTENT)
template <class L0, class L1, class L2>
void
lock(L0& l0, L1& l1, L2& l2)
{
while (true)
{
std::unique_lock<L0> u0(l0);
if (std::try_lock(l1, l2) == -1)
{
u0.release();
break;
}
}
}
#elif defined(ORDERED)
template <class Compare, class ForwardIterator>
void
sort3(ForwardIterator x, ForwardIterator y, ForwardIterator z, Compare c)
{
using std::swap;
if (!c(*y, *x)) // if x <= y
{
if (!c(*z, *y)) // if y <= z
return; // x <= y && y <= z
// x <= y && y > z
swap(*y, *z); // x <= z && y < z
if (c(*y, *x)) // if x > y
swap(*x, *y); // x < y && y <= z
return; // x <= y && y < z
}
if (c(*z, *y)) // x > y, if y > z
{
swap(*x, *z); // x < y && y < z
return;
}
swap(*x, *y); // x > y && y <= z
if (c(*z, *y)) // if y > z
swap(*y, *z); // x <= y && y < z
} // x <= y && y <= z
template <class L0>
void
lock(L0& l0, L0& l1, L0& l2)
{
L0* locks[] = {&l0, &l1, &l2};
sort3(&locks[0], &locks[1], &locks[2],
[](L0* x, L0* y)
{
return x->mutex() < y->mutex();
});
std::unique_lock<L0> u0(*locks[0]);
std::unique_lock<L0> u1(*locks[1]);
locks[2]->lock();
u1.release();
u0.release();
}
#endif
class Philosopher
{
std::mt19937_64 eng_{std::random_device{}()};
std::mutex& left_fork_;
std::mutex& center_fork_;
std::mutex& right_fork_;
std::chrono::milliseconds eat_time_{0};
static constexpr std::chrono::seconds full_{30};
public:
Philosopher(std::mutex& left, std::mutex& center, std::mutex& right);
void dine();
private:
void eat();
std::chrono::milliseconds get_eat_duration();
};
constexpr std::chrono::seconds Philosopher::full_;
Philosopher::Philosopher(std::mutex& left, std::mutex& center, std::mutex& right)
: left_fork_(left)
, center_fork_(center)
, right_fork_(right)
{}
void
Philosopher::dine()
{
while (eat_time_ < full_)
eat();
}
void
Philosopher::eat()
{
using Lock = std::unique_lock<std::mutex>;
std::mutex* mutexes[] = {&left_fork_, ¢er_fork_, &right_fork_};
std::shuffle(std::begin(mutexes), std::end(mutexes), eng_);
Lock first(*mutexes[0], std::defer_lock);
Lock second(*mutexes[1], std::defer_lock);
Lock third(*mutexes[2], std::defer_lock);
auto d = get_eat_duration();
::lock(first, second, third);
auto end = std::chrono::steady_clock::now() + d;
while (std::chrono::steady_clock::now() < end)
;
eat_time_ += d;
}
std::chrono::milliseconds
Philosopher::get_eat_duration()
{
std::uniform_int_distribution<> ms(1, 10);
return std::min(std::chrono::milliseconds(ms(eng_)), full_ - eat_time_);
}
int
main()
{
#ifdef SMART_POLITE
std::cout << "SMART_POLITE\n";
#elif defined(SMART)
std::cout << "SMART\n";
#elif defined(PERSISTENT)
std::cout << "PERSISTENT\n";
#elif defined(ORDERED)
std::cout << "ORDERED\n";
#endif
#if 0
std::cout << "tetrahedron\n";
std::vector<std::mutex> table(6);
std::vector<Philosopher> diners;
diners.push_back(Philosopher(table[0], table[2], table[3]));
diners.push_back(Philosopher(table[0], table[1], table[4]));
diners.push_back(Philosopher(table[1], table[2], table[5]));
diners.push_back(Philosopher(table[3], table[4], table[5]));
#elif 0
std::cout << "cube\n";
std::vector<std::mutex> table(12);
std::vector<Philosopher> diners;
diners.push_back(Philosopher(table[0], table[3], table[4]));
diners.push_back(Philosopher(table[0], table[1], table[5]));
diners.push_back(Philosopher(table[1], table[2], table[6]));
diners.push_back(Philosopher(table[2], table[3], table[7]));
diners.push_back(Philosopher(table[4], table[8], table[11]));
diners.push_back(Philosopher(table[5], table[8], table[9]));
diners.push_back(Philosopher(table[6], table[9], table[10]));
diners.push_back(Philosopher(table[7], table[10], table[11]));
#elif 1
std::cout << "dodecahedron\n";
std::vector<std::mutex> table(30);
std::vector<Philosopher> diners;
diners.push_back(Philosopher(table[0], table[4], table[5]));
diners.push_back(Philosopher(table[0], table[1], table[6]));
diners.push_back(Philosopher(table[1], table[2], table[7]));
diners.push_back(Philosopher(table[2], table[3], table[8]));
diners.push_back(Philosopher(table[3], table[4], table[9]));
diners.push_back(Philosopher(table[5], table[10], table[19]));
diners.push_back(Philosopher(table[10], table[11], table[20]));
diners.push_back(Philosopher(table[6], table[11], table[12]));
diners.push_back(Philosopher(table[12], table[13], table[21]));
diners.push_back(Philosopher(table[7], table[13], table[14]));
diners.push_back(Philosopher(table[14], table[15], table[22]));
diners.push_back(Philosopher(table[8], table[15], table[16]));
diners.push_back(Philosopher(table[16], table[17], table[23]));
diners.push_back(Philosopher(table[9], table[17], table[18]));
diners.push_back(Philosopher(table[18], table[19], table[24]));
diners.push_back(Philosopher(table[20], table[25], table[29]));
diners.push_back(Philosopher(table[21], table[25], table[26]));
diners.push_back(Philosopher(table[22], table[26], table[27]));
diners.push_back(Philosopher(table[23], table[27], table[28]));
diners.push_back(Philosopher(table[24], table[28], table[29]));
#endif
std::vector<std::thread> threads(diners.size());
unsigned i = 0;
auto t0 = std::chrono::high_resolution_clock::now();
for (auto& t : threads)
{
t = std::thread(&Philosopher::dine, diners[i]);
++i;
}
for (auto& t : threads)
t.join();
auto t1 = std::chrono::high_resolution_clock::now();
using secs = std::chrono::duration<float>;
std::cout << secs(t1-t0).count() << '\n';
}
Thanks to Jonathan Wakely for his careful review.